devtools::install_github("LukeCe/spflow")Using github PAT from envvar GITHUB_PATSkipping install of 'spflow' from a github remote, the SHA1 (df913677) has not changed since last install.
Use `force = TRUE` to force installationIn-class_ex5
Overview
Spatial Econometric Interaction Models can be used to overcome the limitations of spatial interaction models that are often used for analysing origin and destination flows. This models are limited to assuming that distance will overshadow spatial dependency between OD flows.
Import package and data
Import packages
Here we will install the development version of spflow package using devtools.
Next we will load the other packages.1
pacman::p_load(tmap,sf,spdep,sp,Matrix,reshape2,knitr, tidyverse, spflow)Import data
Here we will load the data that we will be using for this in class exercise.
Before we can calibrate Spatial Econometric Interaction models by using spflow we need 3 sets of fdata tibble data containing origins, destination, flows and distances between the origin and destination spatial weights tibble data containing explanatory variables
We weill import all of the prepared data for use in this in class exercise 5.
mpsz_nb<-read_rds("data/rds/mpsz_nb.rds")
mpsz_flow<-read_rds("data/rds/mpsz_flow.rds")
mpsz_var<-read_rds("data/rds/mpsz_var.rds")mpsz <- st_read(dsn = "data/geospatial",
layer = "MPSZ-2019") %>%
st_transform(crs = 3414) Reading layer `MPSZ-2019' from data source
`C:\Users\Lian Khye\Desktop\MITB\Geospatial\geartooth\ISSS624\In-class_Ex\Ex5\data\geospatial'
using driver `ESRI Shapefile'
Simple feature collection with 332 features and 6 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 103.6057 ymin: 1.158699 xmax: 104.0885 ymax: 1.470775
Geodetic CRS: WGS 84Creating spflow_network-class objects
spflow_network-class is an S4 class that contains all information on a spatial network which is composed by a set of nodes that are linked by some neighbourhood relation. It can be created by spflow_network() function of spflow package.
For our model, we choose the contiguity based neighbourhood structure.
mpsz_net<- spflow_network(
id_net = "sg",
node_neighborhood =
nb2mat(mpsz_nb$by_contiguity),
node_data= mpsz_var,
node_key_column = "SZ_CODE"
)
mpsz_netSpatial network nodes with id: sg
--------------------------------------------------
Number of nodes: 313
Average number of links per node: 6.077
Density of the neighborhood matrix: 1.94% (non-zero connections)
Data on nodes:
SZ_NAME SZ_CODE BUSSTOP_COUNT AGE7_12 AGE13_24 AGE25_64
1 INSTITUTION HILL RVSZ05 2 330 360 2260
2 ROBERTSON QUAY SRSZ01 10 320 350 2200
3 FORT CANNING MUSZ02 6 0 10 30
4 MARINA EAST (MP) MPSZ05 2 0 0 0
5 SENTOSA SISZ01 1 200 260 1440
6 CITY TERMINALS BMSZ17 10 0 0 0
--- --- --- --- --- --- ---
308 NEE SOON YSSZ07 12 90 140 590
309 UPPER THOMSON BSSZ01 47 1590 3660 15980
310 SHANGRI-LA AMSZ05 12 810 1920 9650
311 TOWNSVILLE AMSZ04 9 980 2000 11320
312 MARYMOUNT BSSZ02 25 1610 4060 16860
313 TUAS VIEW EXTENSION TSSZ06 11 0 0 0
SCHOOL_COUNT BUSINESS_COUNT RETAILS_COUNT FINSERV_COUNT ENTERTN_COUNT
1 1 6 26 3 0
2 0 4 207 18 6
3 0 7 17 0 3
4 0 0 0 0 0
5 0 1 84 29 2
6 0 11 14 4 0
--- --- --- --- --- ---
308 0 0 7 0 0
309 3 21 305 30 0
310 3 0 53 9 0
311 1 0 83 11 0
312 3 19 135 8 0
313 0 53 3 1 0
FB_COUNT LR_COUNT COORD_X COORD_Y
1 4 3 103.84 1.29
2 38 11 103.84 1.29
3 4 7 103.85 1.29
4 0 0 103.88 1.29
5 38 20 103.83 1.25
6 15 0 103.85 1.26
--- --- --- --- ---
308 0 0 103.81 1.4
309 5 11 103.83 1.36
310 0 0 103.84 1.37
311 1 1 103.85 1.36
312 3 11 103.84 1.35
313 0 0 103.61 1.26Creating network pair
Next we will create the network pair object holding information on origin and destination.
mpsz_net_pairs <- spflow_network_pair(
id_orig_net = "sg",
id_dest_net = "sg",
pair_data = mpsz_flow,
orig_key_column = "ORIGIN_SZ",
dest_key_column = "DESTIN_SZ")
mpsz_net_pairsSpatial network pair with id: sg_sg
--------------------------------------------------
Origin network id: sg (with 313 nodes)
Destination network id: sg (with 313 nodes)
Number of pairs: 97969
Completeness of pairs: 100.00% (97969/97969)
Data on node-pairs:
DESTIN_SZ ORIGIN_SZ DISTANCE TRIPS
1 RVSZ05 RVSZ05 0 67
314 SRSZ01 RVSZ05 305.74 251
627 MUSZ02 RVSZ05 951.83 0
940 MPSZ05 RVSZ05 5254.07 0
1253 SISZ01 RVSZ05 4975 0
1566 BMSZ17 RVSZ05 3176.16 0
--- --- --- --- ---
96404 YSSZ07 TSSZ06 26972.97 0
96717 BSSZ01 TSSZ06 25582.48 0
97030 AMSZ05 TSSZ06 26714.79 0
97343 AMSZ04 TSSZ06 27572.74 0
97656 BSSZ02 TSSZ06 26681.7 0
97969 TSSZ06 TSSZ06 0 270Creating spflow_network_multi-class object
The sp_multi_network class combines information on the nodes and the node-pairs and also ensures that both data sources are consistent. For example, if some of the origins in the sp_network_pair-class are not identified with the nodes in the sp_network_nodes-class an error will be raised.
mpsz_multi_net <- spflow_network_multi(mpsz_net,
mpsz_net_pairs)
mpsz_multi_netCollection of spatial network nodes and pairs
--------------------------------------------------
Contains 1 spatial network nodes
With id : sg
Contains 1 spatial network pairs
With id : sg_sg
Availability of origin-destination pair information:
ID_ORIG_NET ID_DEST_NET ID_NET_PAIR COMPLETENESS C_PAIRS C_ORIG C_DEST
sg sg sg_sg 100.00% 97969/97969 313/313 313/313We can then plot a geographical representation of the flow.
plot(mpsz$geometry)
spflow_map(
mpsz_multi_net,
flow_var = "TRIPS",
add = TRUE,
legend_position = "bottomleft",
filter_lowest = .999,
remove_intra = TRUE,
cex = 1)Correlation analysis
Multicollinearity refers to a situation in which more than 2 explanatory variables in a multiple regression model are highly linearly related. In this situation, the coefficient estimates of the multiple regression may change erratically in response to small changes in the data or the procedure used to fit the model.
spflow provides pair_cor() and cor_image() to create a correlation matrix and to plot the correlation matrix as a correlogram.
cor_formula <- log(1+TRIPS) ~
BUSSTOP_COUNT +
AGE7_12 +
AGE13_24+
AGE25_64+
SCHOOL_COUNT+
BUSINESS_COUNT+
RETAILS_COUNT+
FINSERV_COUNT+
P_(log(DISTANCE+1))
cor_mat<-pair_cor(
mpsz_multi_net,
spflow_formula = cor_formula,
add_lags_x = FALSE)
colnames(cor_mat) <- paste0(
substr(
colnames(cor_mat),1,3),"...")
cor_image(cor_mat)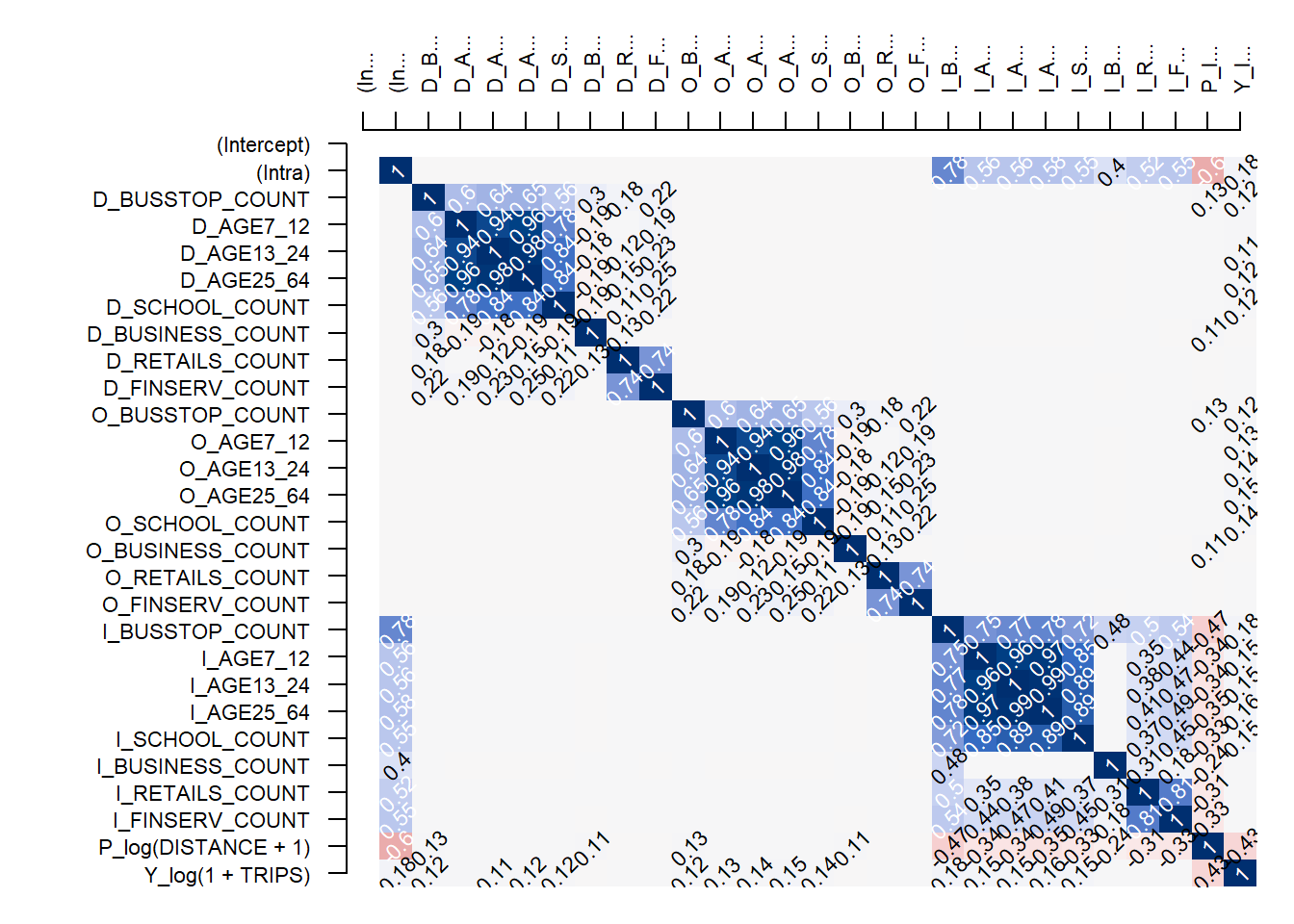
Model calibration
There are 3 different estimators of spatial econometric interaction models which are: - Maximum likelihood estimation - Spatial two-stage least squares - Bayesian Markov chain Monte Carlo
Base model
Here we will calibrate a base model using: - Explanatory variables: BUSSTOP_COUNT and AGE25_64 - Explanatory variables: SCHOOL_COUNT, BUSINESS_COUNT, RETAILS_COUNT, FINSERV_COUNT - Explanatory variables for O-D pairs: DISTANCE
base_model <- spflow(
spflow_formula = log(1+TRIPS) ~
O_(BUSSTOP_COUNT +
AGE25_64) +
D_(SCHOOL_COUNT+
BUSINESS_COUNT+
RETAILS_COUNT+
FINSERV_COUNT) +
P_(log(DISTANCE + 1)),
spflow_networks = mpsz_multi_net
)
base_model--------------------------------------------------
Spatial interaction model estimated by: MLE
Spatial correlation structure: SDM (model_9)
Dependent variable: log(1 + TRIPS)
--------------------------------------------------
Coefficients:
est sd t.stat p.val
rho_d 0.680 0.004 192.554 0.000
rho_o 0.678 0.004 187.732 0.000
rho_w -0.396 0.006 -65.590 0.000
(Intercept) 0.410 0.065 6.266 0.000
(Intra) 1.313 0.081 16.263 0.000
D_SCHOOL_COUNT 0.017 0.002 7.885 0.000
D_SCHOOL_COUNT.lag1 0.002 0.004 0.551 0.581
D_BUSINESS_COUNT 0.000 0.000 3.015 0.003
D_BUSINESS_COUNT.lag1 0.000 0.000 -0.249 0.804
D_RETAILS_COUNT 0.000 0.000 -0.306 0.759
D_RETAILS_COUNT.lag1 0.000 0.000 0.152 0.880
D_FINSERV_COUNT 0.002 0.000 6.787 0.000
D_FINSERV_COUNT.lag1 -0.002 0.001 -3.767 0.000
O_BUSSTOP_COUNT 0.002 0.000 6.806 0.000
O_BUSSTOP_COUNT.lag1 -0.001 0.000 -2.364 0.018
O_AGE25_64 0.000 0.000 7.336 0.000
O_AGE25_64.lag1 0.000 0.000 -2.797 0.005
P_log(DISTANCE + 1) -0.050 0.007 -6.793 0.000
--------------------------------------------------
R2_corr: 0.6942944
Observations: 97969
Model coherence: ValidatedWe see that the about 69% of all trip variations can be explained by the model.
plot(base_model)
Residual diagnostics
To check if the model calibrated follows the statistical assumption of the methods used, we can use the spflow package to do so.
old_par <- par(mfrow = c(1,3),
mar = c(2,2,2,2))
spflow_moran_plots(base_model)
par(old_par)Next, pair_cor() can be used to inspect the relationship of the residual and the explanatory variables and we will re run the correlogram.
corr_residual <- pair_cor(base_model)
colnames(corr_residual) <- substr(colnames(corr_residual),1,3)
cor_image(corr_residual)
model.df <- as_tibble(base_model@spflow_indicators) %>%
mutate(FITTED_Y = round(exp(FITTED),0))
mpsz_flow1 <- mpsz_flow %>%
left_join(model.df) %>%
select(1:4,8) %>%
mutate(diff = (FITTED_Y-TRIPS))Joining with `by = join_by(ORIGIN_SZ, DESTIN_SZ)`Model control
We can use the different models listed here to check. Here we will try model 1, 8 and 9.
Model 1
spflow_formula <- log(1+TRIPS)~
O_(BUSSTOP_COUNT +
AGE25_64) +
D_(SCHOOL_COUNT+
BUSINESS_COUNT+
RETAILS_COUNT+
FINSERV_COUNT) +
P_(log(DISTANCE + 1))
model_control <- spflow_control(
estimation_method = "mle",
model = "model_1")
mle_model1 <- spflow(
spflow_formula,
spflow_networks = mpsz_multi_net,
estimation_control = model_control
)
mle_model1--------------------------------------------------
Spatial interaction model estimated by: OLS
Spatial correlation structure: SLX (model_1)
Dependent variable: log(1 + TRIPS)
--------------------------------------------------
Coefficients:
est sd t.stat p.val
(Intercept) 11.384 0.069 164.255 0.000
(Intra) -6.006 0.112 -53.393 0.000
D_SCHOOL_COUNT 0.093 0.003 28.599 0.000
D_SCHOOL_COUNT.lag1 0.255 0.006 44.905 0.000
D_BUSINESS_COUNT 0.001 0.000 10.036 0.000
D_BUSINESS_COUNT.lag1 0.003 0.000 18.274 0.000
D_RETAILS_COUNT 0.000 0.000 -1.940 0.052
D_RETAILS_COUNT.lag1 0.000 0.000 -2.581 0.010
D_FINSERV_COUNT 0.005 0.000 10.979 0.000
D_FINSERV_COUNT.lag1 -0.016 0.001 -17.134 0.000
O_BUSSTOP_COUNT 0.014 0.001 25.865 0.000
O_BUSSTOP_COUNT.lag1 0.015 0.001 21.728 0.000
O_AGE25_64 0.000 0.000 14.479 0.000
O_AGE25_64.lag1 0.000 0.000 14.452 0.000
P_log(DISTANCE + 1) -1.281 0.008 -165.327 0.000
--------------------------------------------------
R2_corr: 0.2831458
Observations: 97969
Model coherence: ValidatedThis represents our unconstrained model and a Rsquare of only about 28%.
old_par <- par(mfrow = c(1, 3),
mar = c(2,2,2,2))
spflow_moran_plots(mle_model1)
Model 8
model_control <- spflow_control(
estimation_method = "mle",
model = "model_8")
mle_model8 <- spflow(
spflow_formula,
spflow_networks = mpsz_multi_net,
estimation_control = model_control
)
mle_model8--------------------------------------------------
Spatial interaction model estimated by: MLE
Spatial correlation structure: SDM (model_8)
Dependent variable: log(1 + TRIPS)
--------------------------------------------------
Coefficients:
est sd t.stat p.val
rho_d 0.689 0.003 196.833 0.000
rho_o 0.687 0.004 192.213 0.000
rho_w -0.473 0.003 -142.469 0.000
(Intercept) 1.086 0.049 22.275 0.000
(Intra) 0.840 0.075 11.255 0.000
D_SCHOOL_COUNT 0.019 0.002 8.896 0.000
D_SCHOOL_COUNT.lag1 0.019 0.004 5.130 0.000
D_BUSINESS_COUNT 0.000 0.000 3.328 0.001
D_BUSINESS_COUNT.lag1 0.000 0.000 1.664 0.096
D_RETAILS_COUNT 0.000 0.000 -0.414 0.679
D_RETAILS_COUNT.lag1 0.000 0.000 -0.171 0.864
D_FINSERV_COUNT 0.002 0.000 6.150 0.000
D_FINSERV_COUNT.lag1 -0.003 0.001 -4.601 0.000
O_BUSSTOP_COUNT 0.003 0.000 7.676 0.000
O_BUSSTOP_COUNT.lag1 0.000 0.000 0.552 0.581
O_AGE25_64 0.000 0.000 6.870 0.000
O_AGE25_64.lag1 0.000 0.000 -0.462 0.644
P_log(DISTANCE + 1) -0.125 0.005 -22.865 0.000
--------------------------------------------------
R2_corr: 0.6965975
Observations: 97969
Model coherence: ValidatedModel 8 contains intra-zonal data and have a R square of 0.69
old_par <- par(mfrow = c(1,3),
mar = c(2,2,2,2))
spflow_moran_plots(mle_model8)
par(old_par)Model 9
model_control <- spflow_control(
estimation_method = "mle",
model = "model_9")
mle_model9 <- spflow(
spflow_formula,
spflow_networks = mpsz_multi_net,
estimation_control = model_control
)
mle_model9--------------------------------------------------
Spatial interaction model estimated by: MLE
Spatial correlation structure: SDM (model_9)
Dependent variable: log(1 + TRIPS)
--------------------------------------------------
Coefficients:
est sd t.stat p.val
rho_d 0.680 0.004 192.554 0.000
rho_o 0.678 0.004 187.732 0.000
rho_w -0.396 0.006 -65.591 0.000
(Intercept) 0.410 0.065 6.266 0.000
(Intra) 1.313 0.081 16.263 0.000
D_SCHOOL_COUNT 0.017 0.002 7.885 0.000
D_SCHOOL_COUNT.lag1 0.002 0.004 0.551 0.581
D_BUSINESS_COUNT 0.000 0.000 3.015 0.003
D_BUSINESS_COUNT.lag1 0.000 0.000 -0.249 0.804
D_RETAILS_COUNT 0.000 0.000 -0.306 0.759
D_RETAILS_COUNT.lag1 0.000 0.000 0.152 0.880
D_FINSERV_COUNT 0.002 0.000 6.787 0.000
D_FINSERV_COUNT.lag1 -0.002 0.001 -3.767 0.000
O_BUSSTOP_COUNT 0.002 0.000 6.806 0.000
O_BUSSTOP_COUNT.lag1 -0.001 0.000 -2.364 0.018
O_AGE25_64 0.000 0.000 7.336 0.000
O_AGE25_64.lag1 0.000 0.000 -2.797 0.005
P_log(DISTANCE + 1) -0.050 0.007 -6.793 0.000
--------------------------------------------------
R2_corr: 0.6942946
Observations: 97969
Model coherence: ValidatedWe can see that model 9 has the highest R-square value of the 3 models that we tested.
old_par <- par(mfrow = c(1, 3),
mar = c(2,2,2,2))
spflow_moran_plots(mle_model9)